Starting in the top left corner of a 2×2 grid, and only being able to move
to the right and down, there are exactly 6 routes to the bottom right corner.
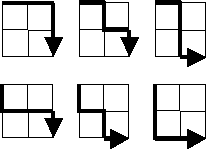
How many such routes are there through a 20×20 grid?
The trick I found for this is that the number of paths is the same as the
numbers of a Pascal's Triangle. The numbers of the square formed by the
triangle correspond to possible paths to corresponding nodes.
I used some for loops and an array of arrays to make a Pascal's Triangle
that corresponded to a 20 × 20 square and returned the value at the terminal
node.
###,###